[5]:

from hestonpy.models.heston import Heston
from hestonpy.models.bates import Bates
from hestonpy.models.calibration.volatilitySmile import VolatilitySmile

r = 0.00

Calibration on market data#

Get market data

[6]:

from hestonpy.option.data import get_options_data, filter_data_for_maturity
symbol='^SPX'
all_market_data, spot, maturities = get_options_data(symbol=symbol)
spot

[6]:

np.float64(5396.52001953125)

Choose your smile/maturity

[7]:

maturities

[7]:

('2025-04-04',
 '2025-04-07',
 '2025-04-08',
 '2025-04-09',
 '2025-04-10',
 '2025-04-11',
 '2025-04-14',
 '2025-04-15',
 '2025-04-16',
 '2025-04-17',
 '2025-04-21',
 '2025-04-22',
 '2025-04-23',
 '2025-04-24',
 '2025-04-25',
 '2025-04-28',
 '2025-04-29',
 '2025-04-30',
 '2025-05-01',
 '2025-05-02',
 '2025-05-05',
 '2025-05-06',
 '2025-05-08',
 '2025-05-09',
 '2025-05-16',
 '2025-05-30',
 '2025-06-20',
 '2025-06-30',
 '2025-07-18',
 '2025-07-31',
 '2025-08-15',
 '2025-08-29',
 '2025-09-19',
 '2025-09-30',
 '2025-10-17',
 '2025-11-21',
 '2025-12-19',
 '2025-12-31',
 '2026-01-16',
 '2026-02-20',
 '2026-03-20',
 '2026-03-31',
 '2026-04-17',
 '2026-06-18',
 '2026-12-18',
 '2027-12-17',
 '2028-12-15',
 '2029-12-21',
 '2030-12-20')

[8]:

maturity = maturities[28]
full_market_data = filter_data_for_maturity(all_market_data, maturity)
full_market_data.head()

[8]:
Call Price Bid Ask Implied Volatility Strike Volume Time to Maturity Maturity
0 5357.61 5133.6 5145.5 0.000010 200.0 1.0 0.297619 2025-07-18
1 5062.65 5188.8 5206.3 5.966830 800.0 2.0 0.297619 2025-07-18
2 4589.30 4345.0 4362.7 0.000010 1000.0 1.0 0.297619 2025-07-18
3 4676.42 4797.4 4815.3 4.155095 1200.0 18.0 0.297619 2025-07-18
4 4500.20 4605.1 4620.0 3.680169 1400.0 1.0 0.297619 2025-07-18

Sanity check of the data from yfinance

[9]:

time_to_maturity = full_market_data['Time to Maturity'].iloc[0]
strikes = full_market_data['Strike'].values
bid_prices = full_market_data["Bid"].values
ask_prices = full_market_data['Ask'].values
market_ivs = full_market_data['Implied Volatility'].values
market_prices = full_market_data['Call Price'].values

marketVolatilitySmile = VolatilitySmile(
    strikes=strikes,
    time_to_maturity=time_to_maturity,
    atm=spot,
    market_ivs=market_ivs,
    r=r
)
marketVolatilitySmile.plot(bid_prices=bid_prices, ask_prices=ask_prices)
../../_images/examples_calibration_calibration_real_data_8_0.png

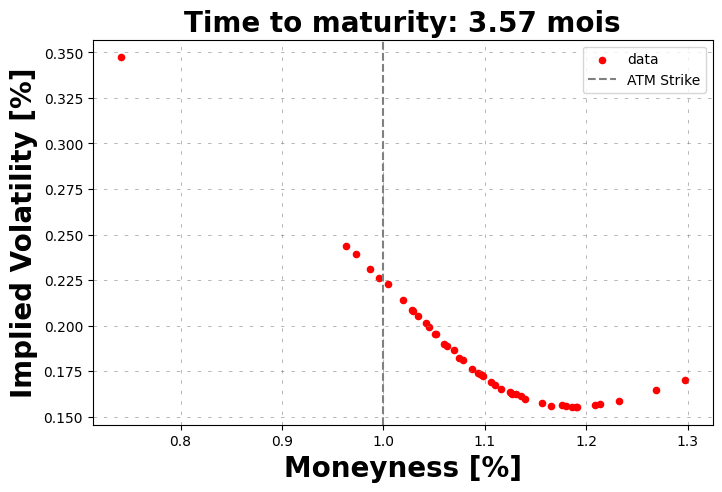
Hmmm it is ugly, run some filters and use the mid implied volatility to denoise the market,

\[\frac{\sigma_{bid}+\sigma_{ask}}{2}\]
[10]:

market_data = marketVolatilitySmile.filters(full_market_data)
marketVolatilitySmile.plot()
market_data.head()
../../_images/examples_calibration_calibration_real_data_10_0.png 
[10]:
Call Price Bid Ask Implied Volatility Strike Volume Time to Maturity Maturity Mid ivs Ask ivs Bid ivs Mid Price
13 1474.75 1411.0 1426.2 0.377997 4000.0 731.0 0.297619 2025-07-18 0.347358 0.373705 0.321010 1418.60
39 429.56 389.0 391.4 0.247988 5200.0 40.0 0.297619 2025-07-18 0.243961 0.245046 0.242876 390.20
42 393.78 354.8 358.3 0.243847 5250.0 40.0 0.297619 2025-07-18 0.239403 0.240951 0.237855 356.55
46 467.57 305.5 307.8 0.234829 5325.0 38.0 0.297619 2025-07-18 0.231043 0.232036 0.230050 306.65
49 376.33 274.5 276.9 0.229813 5375.0 250.0 0.297619 2025-07-18 0.226052 0.227078 0.225026 275.70

We can now calibrate an Heston model and an Bates model on the cleaned data

Calibration with an Heston model#

[11]:

params = {
    "kappa": 1.25,
    "theta": 0.06,
    "sigma": 0.6,
    "rho": -0.8,
}
heston = Heston(spot=spot, vol_initial=0.06, r=r, drift_emm=0, **params)

initial_params = marketVolatilitySmile.calibration(
    price_function=heston.call_price,
    guess_correlation_sign='negative',
    initial_guess=list(params.values()),
    speed='local',
)

initial_guess = [initial_params['kappa'], initial_params['theta'], initial_params['sigma'], initial_params['rho']]
calibrated_params = marketVolatilitySmile.calibration(
    price_function=heston.call_price,
    guess_correlation_sign='negative',
    initial_guess=initial_guess,
    power='mse',
    speed='global',
)

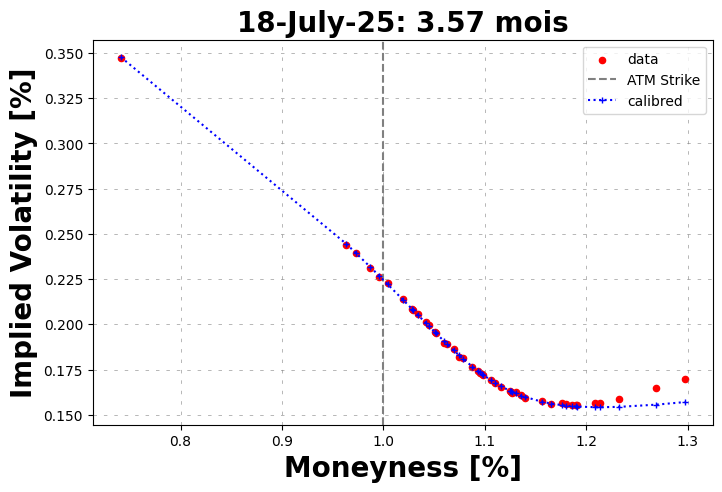
marketVolatilitySmile.plot(
    calibrated_prices=heston.call_price(strike=marketVolatilitySmile.strikes, time_to_maturity=time_to_maturity, **calibrated_params),
    maturity=maturity
)
calibrated_params

Calibrated parameters: v0=0.051 | kappa=0.582 | theta=0.182 | sigma=0.708 | rho=-0.817

at minimum 0.180315 accepted 1
Parameters: kappa=0.582 | theta=0.182 | sigma=0.708 | rho=-0.817

at minimum 0.180315 accepted 1
Parameters: kappa=0.582 | theta=0.182 | sigma=0.708 | rho=-0.817

at minimum 0.180315 accepted 1
Parameters: kappa=0.582 | theta=0.182 | sigma=0.708 | rho=-0.817

at minimum 0.180315 accepted 1
Parameters: kappa=0.582 | theta=0.182 | sigma=0.708 | rho=-0.817

at minimum 0.180315 accepted 1
Parameters: kappa=0.582 | theta=0.182 | sigma=0.708 | rho=-0.817

at minimum 0.180315 accepted 1
Parameters: kappa=0.582 | theta=0.182 | sigma=0.708 | rho=-0.817

at minimum 0.180315 accepted 1
Parameters: kappa=0.582 | theta=0.182 | sigma=0.708 | rho=-0.817

at minimum 0.180324 accepted 1
Parameters: kappa=0.594 | theta=0.179 | sigma=0.709 | rho=-0.817

at minimum 0.180315 accepted 1
Parameters: kappa=0.582 | theta=0.182 | sigma=0.708 | rho=-0.817

at minimum 0.180315 accepted 1
Parameters: kappa=0.582 | theta=0.182 | sigma=0.708 | rho=-0.817

['success condition satisfied'] True
Calibrated parameters: v0=0.051 | kappa=0.582 | theta=0.182 | sigma=0.708 | rho=-0.817
../../_images/examples_calibration_calibration_real_data_13_1.png 
[11]:

{'vol_initial': np.float64(0.05109935754345381),
 'kappa': np.float64(0.5815576684696807),
 'theta': np.float64(0.1816239411613502),
 'sigma': np.float64(0.707675064288899),
 'rho': np.float64(-0.8170984923714757),
 'drift_emm': 0}

Calibration with a Baites model#

[12]:

calibrated_params

[12]:

{'vol_initial': np.float64(0.05109935754345381),
 'kappa': np.float64(0.5815576684696807),
 'theta': np.float64(0.1816239411613502),
 'sigma': np.float64(0.707675064288899),
 'rho': np.float64(-0.8170984923714757),
 'drift_emm': 0}

[15]:

params = {
    "kappa": 1.25,
    "theta": 0.06,
    "sigma": 0.6,
    "rho": -0.5,
    "lambda_jump": 1.0,
    "mu_J": -0.1,
    'sigma_J': 0.3
}

bates = Bates(spot=spot, vol_initial=0.06, r=r, drift_emm=0, **params)

initial_params = marketVolatilitySmile.calibration(
    price_function=bates.call_price,
    guess_correlation_sign='negative',
    initial_guess=list(params.values()),
    power='mse',
    speed='local',
)

initial_guess = [initial_params['kappa'], initial_params['theta'], initial_params['sigma'], initial_params['rho'],
                 initial_params['lambda_jump'], initial_params['mu_J'], initial_params['sigma_J']]
calibrated_params = marketVolatilitySmile.calibration(
    price_function=bates.call_price,
    guess_correlation_sign='negative',
    initial_guess=initial_guess,
    power='mse',
    speed='global',
)

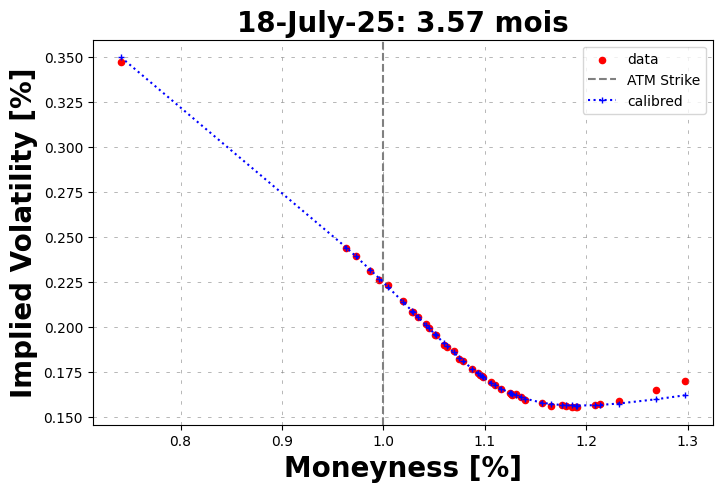
marketVolatilitySmile.plot(
    calibrated_prices=bates.call_price(strike=marketVolatilitySmile.strikes, time_to_maturity=time_to_maturity, **calibrated_params),
    maturity=maturity
)
calibrated_params

Calibrated parameters:
 v0=0.051 | kappa=1.170 | theta=0.086 | sigma=0.802 | rho=-0.796  | lambda_jump=0.569  | mu_J=-0.087  | sigma_J=0.050

at minimum 0.138248 accepted 1
Parameters: kappa=1.170 | theta=0.086 | sigma=0.802 | rho=-0.796  | lambda_jump=0.569  | mu_J=-0.087  | sigma_J=0.050

at minimum 0.137477 accepted 1
Parameters: kappa=1.816 | theta=0.070 | sigma=0.865 | rho=-0.786  | lambda_jump=0.509  | mu_J=-0.108  | sigma_J=0.050

at minimum 0.137710 accepted 1
Parameters: kappa=1.518 | theta=0.076 | sigma=0.836 | rho=-0.790  | lambda_jump=0.526  | mu_J=-0.099  | sigma_J=0.050

at minimum 0.137298 accepted 1
Parameters: kappa=2.585 | theta=0.060 | sigma=0.944 | rho=-0.774  | lambda_jump=0.510  | mu_J=-0.122  | sigma_J=0.050

at minimum 0.137585 accepted 1
Parameters: kappa=1.651 | theta=0.073 | sigma=0.848 | rho=-0.788  | lambda_jump=0.516  | mu_J=-0.103  | sigma_J=0.050

at minimum 0.137499 accepted 1
Parameters: kappa=1.773 | theta=0.070 | sigma=0.861 | rho=-0.786  | lambda_jump=0.510  | mu_J=-0.107  | sigma_J=0.050

at minimum 0.137303 accepted 1
Parameters: kappa=2.893 | theta=0.057 | sigma=0.977 | rho=-0.770  | lambda_jump=0.514  | mu_J=-0.126  | sigma_J=0.050

at minimum 0.177881 accepted 1
Parameters: kappa=0.002 | theta=2.682 | sigma=0.530 | rho=-0.786  | lambda_jump=0.063  | mu_J=-0.413  | sigma_J=0.050

['success condition satisfied'] True
Calibrated parameters:
 v0=0.051 | kappa=2.585 | theta=0.060 | sigma=0.944 | rho=-0.774  | lambda_jump=0.510  | mu_J=-0.122  | sigma_J=0.050
../../_images/examples_calibration_calibration_real_data_16_1.png 
[15]:

{'vol_initial': np.float64(0.05109935754345381),
 'kappa': np.float64(2.5854664613188842),
 'theta': np.float64(0.059849220476281995),
 'drift_emm': 0,
 'sigma': np.float64(0.9439656148672756),
 'rho': np.float64(-0.7743390297835321),
 'lambda_jump': np.float64(0.5102923508017523),
 'mu_J': np.float64(-0.12185194574808611),
 'sigma_J': np.float64(0.05)}

Fancy plot

[16]:

from datetime import datetime
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.font_manager as font_manager
font_legend = font_manager.FontProperties(
    style='normal',
    size=20,
)
fontdict = {
    "fontsize": 20,
    # "fontweight": "bold"
}
fontdict_suptitle = {
    'fontsize': 30,
    'fontweight': 'bold'
    }
fontdict_title = {
    'fontsize': 30,
    'fontweight': 'bold'
    }

calibrated_prices = bates.call_price(strike=marketVolatilitySmile.strikes, time_to_maturity=time_to_maturity, **calibrated_params)
calibrated_ivs = marketVolatilitySmile.compute_smile(prices=calibrated_prices)
ask_ivs = market_data['Ask ivs'].values
bid_ivs = market_data['Bid ivs'].values
forward = marketVolatilitySmile.atm * np.exp(marketVolatilitySmile.r * marketVolatilitySmile.time_to_maturity)

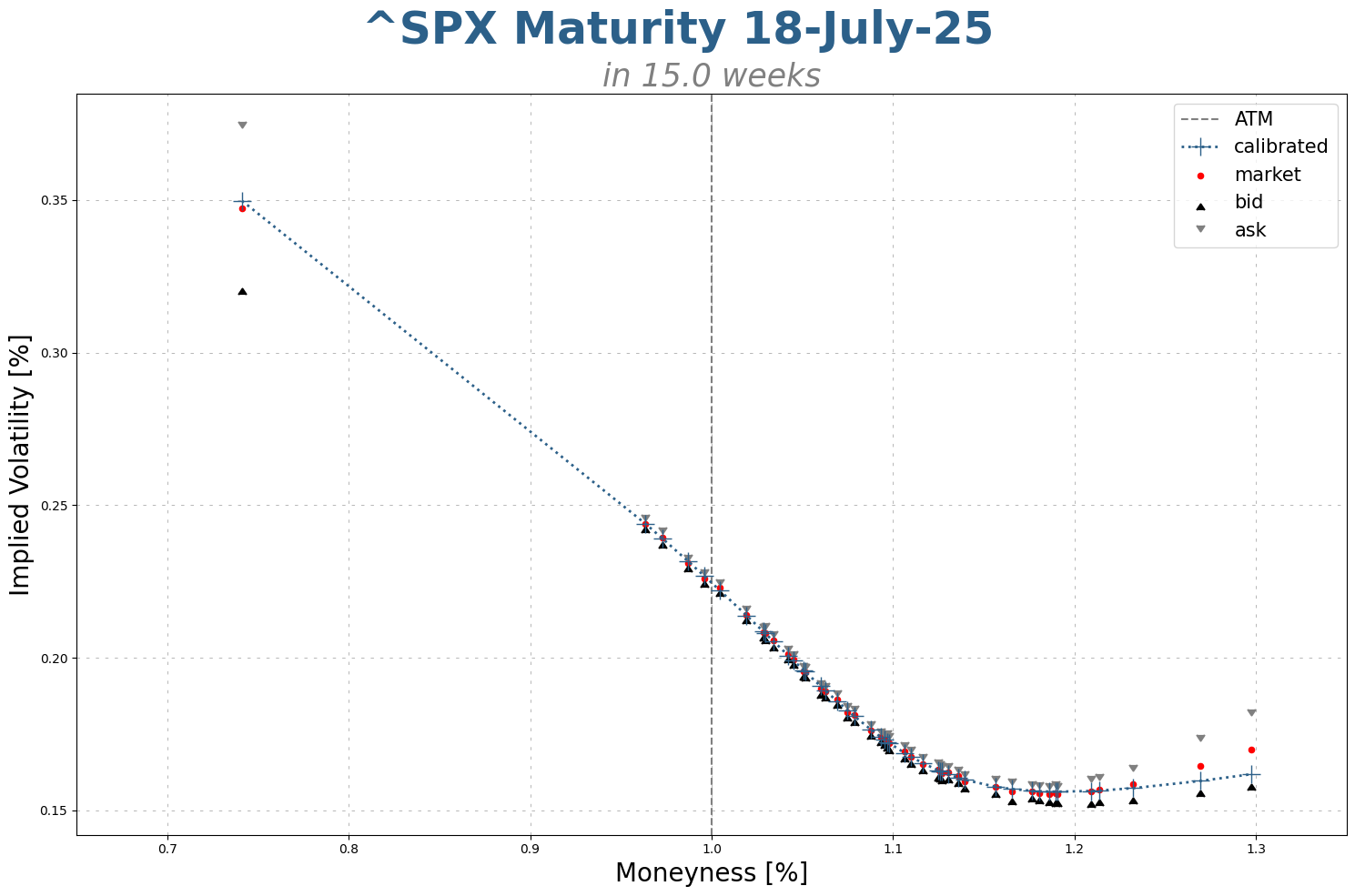
plt.figure(figsize=(15, 10))
plt.axvline(1, linestyle="--", color="gray", label='ATM')
plt.plot(marketVolatilitySmile.strikes / forward, calibrated_ivs, marker='+', color='#2c6089', linestyle="dotted", markersize=14, linewidth=2, label='calibrated')
plt.scatter(marketVolatilitySmile.strikes / forward, marketVolatilitySmile.market_ivs, marker='o', color='red', s=20, label='market')
plt.scatter(marketVolatilitySmile.strikes / forward, bid_ivs, marker=6, color='black', s=40, label='bid')
plt.scatter(marketVolatilitySmile.strikes / forward, ask_ivs, marker=7, color='gray', s=40, label='ask')

plt.xlabel("Moneyness [%]", fontdict=fontdict)
plt.ylabel("Implied Volatility [%]", fontdict=fontdict)
plt.xlim((0.65, 1.35))

date = datetime.strptime(maturity, '%Y-%m-%d').date().strftime("%d-%B-%y")
title = f"{symbol} Maturity {date}"
plt.suptitle(title, fontsize=35, fontweight='bold', color='#2c6089')
plt.title(f"in {marketVolatilitySmile.time_to_maturity * 252 / 5:.1f} weeks", color="grey", style='italic', fontsize=25)

plt.grid(visible=True, which="major", linestyle="--", dashes=(5, 10), color="gray", linewidth=0.5, alpha=0.8)
plt.legend(fontsize=15)
plt.tight_layout()
plt.show()
../../_images/examples_calibration_calibration_real_data_18_0.png